Desviación estándar
De Wikipedia, la enciclopedia libre

La desviación estándar (o desviación típica) es una medida de dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva. Es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.
Para abordar las cuestiones que comentábamos en el párrafo anterior, nos valemos de herramientas como la varianza y la desviación estándar. Ambas medidas están estrechamente relacionadas ya que definimos una a partir de la otra.
Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que representan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad a la hora de describirlos e interpretarlos para la toma de decisiones.
Tabla de contenidos[ocultar] |
Formulación [editar]
La varianza representa la media aritmética de las desviaciones con respecto a la media elevadas al cuadrado. Si atendemos a la colección completa de datos (la población en su totalidad) obtenemos la varianza poblacional; y si por el contrario prestamos atención sólo a una muestra de la población, obtenemos en su lugar la varianza muestral. Las expresiones de estas medidas son las que aparecen a continuación.
Expresión de la varianza muestral:
Expresión de la varianza poblacional:
Una vez entendida la f Expresión de la desviación estándar poblacional:
El término desviación estándar fue incorporado a la estadística por Karl Pearson en 1894.
Por la formulación de la varianza podemos pasar a obtener la desviación estándar, tomando la raíz cuadrada positiva de la varianza. Así, si efectuamos la raíz de la varianza muestral, obtenemos la desviación típica muestral; y si por el contrario, efectuamos la raíz sobre la varianza poblacional, obtendremos la desviación típica poblacional.
Expresión de la desviación estándar muestral:
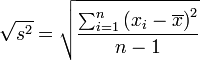 También puede ser tomada como
También puede ser tomada como
con a como  y s como
y s como 
Interpretación y aplicación [editar]
La desviación estándar es una medida del grado de dispersión de los datos del valor promedio. Dicho de otra manera, la desviación estándar es simplemente el "promedio" o variación esperada con respecto de la media aritmética.
Una desviación estándar grande indica que los puntos están lejos de la media, y una desviación pequeña indica que los datos están agrupados cerca a la media.
Por ejemplo, las tres muestras (0, 0, 14, 14), (0, 6, 8, 14) y (6, 6, 8, 8) cada una tiene una media de 7. Sus desviaciones estándar son 7, 4 y 1, respectivamente. La tercera muestra tiene una desviación mucho menor que las otras dos porque sus valores están más cerca de 7.
La desviación estándar puede ser interpretada como una medida de incertidumbre. La desviación estándar de un grupo repetido de medidas nos da la precisión de éstas. Cuando se va a determinar si un grupo de medidas está de acuerdo con el modelo teórico, la desviación estándar de esas medidas es de vital importancia: si la media de las medidas está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces consideramos que las medidas contradicen la teoría. Esto es coherente, ya que las mediciones caen fuera del rango de valores en el cual sería razonable esperar que ocurrieran si el modelo teórico fuera correcto. La desviación estándar es uno de tres parámetros de ubicación central; muestra la agrupación de los datos alrededor de un valor central (la media o promedio).
Desglose [editar]
La desviación estándar (DS/DE), también llamada como desviación típica, es una medida de dispersión usada en estadística que nos dice cuánto tienden a alejarse los valores puntuales del promedio en una distribución. De hecho, específicamente, la desviación estándar es "el promedio de la distancia de cada punto respecto del promedio". Se suele representar por una S o con la letra sigma,  .
.
La desviación estándar de un conjunto de datos es una medida de cuánto se desvían los datos de su media. Esta medida es más estable que el recorrido y toma en consideración el valor de cada dato.
Es posible calcular la desviación estándar de una variable aleatoria continua como la raíz cuadrada de la integral
donde
- La DS es la raíz cuadrada de la varianza de la distribución
Así la varianza es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución.
Aunque esta fórmula es correcta, en la práctica interesa realizar inferencias poblacionales, por lo que en el denominador en vez de n, se usa n-1 (Corrección de Bessel)
También hay otra función más sencilla de realizar y con menos riesgo de tener equivocaciones :
Ejemplo [editar]
Aquí se muestra cómo calcular la desviación estándar de un conjunto de datos. Los datos representan la edad de los miembros de un grupo de niños. { 4, 1, 11, 13, 2, 7 }
1. Calcular el promedio o media aritmética  .
.
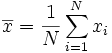 .
.
En este caso, N = 6 porque hay seis datos:
i=número de datos para sacar desviación estándar
 Sustituyendo N por 6
Sustituyendo N por 6
 Este es el promedio.
Este es el promedio.
2. Calcular la desviación estándar 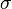
 Sustituyendo N - 1 por 5 ( 6 - 1 )
Sustituyendo N - 1 por 5 ( 6 - 1 )
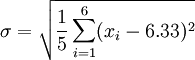 Sustituyendo
Sustituyendo  por 6.33
por 6.33
 Esta es la desviación estándar.
Esta es la desviación estándar.


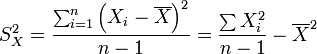








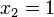






![\sigma = \sqrt{\frac{1}{5} \left [ (4 - 6.33)^2 + (1 - 6.33)^2 + (11 - 6.33)^2 + (13 - 6.33)^2 +(2 - 6.33)^2 + (7 - 6.33)^2 \right ] }](http://upload.wikimedia.org/math/d/0/8/d08b4115380426cec1d166c8089cc5e4.png)
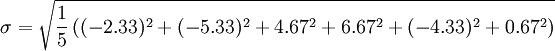

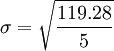
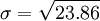

0 comentarios:
Publicar un comentario